Глава 6. ЗНАЧИМЫЕ РЕЗУЛЬТАТЫ
Автор: Роберт ГоттсданкерОпубликовано: January 4, 2005, 12:35 am
Роберт Готтсданкер: Основы Психологического Эксперимента
Давайте рассмотрим две группы результатов, полученных Флинером и Кернсом (1970) в эксперименте, описанном в предыдущей главе, где сравнивались сила и продолжительность плача детей при уходе матери и ассистентки экспериментатора. Плач каждого ребенка оценивался в течение 24 периодов по 5 с как после ухода матери, так и после ухода ассистентки. 15 детей в возрасте от 12 до 14 мес плакали в среднем во времени 11,67 из этих 5-секундных периодов, когда уходила мать; когда же уходила ассистентка, эти дети плакали во время 8,27 таких периодов. На основе средней разницы в 3,40 Флинер и Кернc заключили, что дети указанной возрастной группы плачут больше, когда уходит мать.
В младшей группе, состоящей из 13 детей в возрасте от 9 до 11 меc, аналогичные средние данные оказались: 9,08, когда уходила мать, и 8,15, когда уходила ассистентка. Флинер и Кернc (1970) сделали вывод, что это небольшое различие — всего лишь 0,93 — незначимо. Их вывод, несомненно, представляется правильным, ибо разница действительно очень мала. Но достаточно ли велика была разница между 11,67 и 8,27 для более старшей группы, чтобы подтвердить вывод о значимом различии? Откуда экспериментаторы знают, какова должна быть разница между двумя условиями, чтобы ее можно было принять как значимую?
Логика их рассуждений была несложной. Они понимали, что разница для старшей группы может оказаться случайной. Как мы уже отмечали, есть много причин, по которым с течением времени может изменяться поведение как одного индивида, так в среднем и целой группы. В любом частном эксперименте более сильный плач при уходе матери мог быть случайным. Да, случайное различие было возможно, но — мало вероятно. Исследователи имели возможность вывести, что такое или большее различие возможно не более чем в одном эксперименте из 20. Их устраивала эта оценка, и они отвергли предположение о том, что их эксперимент был как раз тот самый 1 из 20.
С другой стороны, для более младшей группы разница между 9,08 и 8,15 могла оказаться случайной более чем в 1 опыте из 20. И экспериментаторы, таким образом, приняли ее за случайную.
Мы увидим в этой главе, что Флинер и Кернc (1970) проверяли нуль-гипотезу, состоящую в том, что экспериментальные условия не различаются. Термин «нуль» в данном случае означает нулевое различие. В случае со старшими детьми они отвергли нуль-гипотезу, в случае с более младшими — нет.
Такое действие называется проверкой на значимость или на статистическую значимость. Когда нуль-гипотеза отвергается, то говорят, что различие статистически значимо; когда нуль-гипотеза не отвергается, то говорят, что различие (статистически) незначимо.
Мы увидим, что статистическое решение, принять иди отвергнуть нуль-гипотезу, всегда таит в себе двоякий риск. Мы рассмотрим, как подобные статистические решения приводят к выводам относительно экспериментальной гипотезы. При этом мы снова обратимся к понятию внутренней валидности, и далее — к более специальному понятию — надежности.
Наконец, мы попытаемся показать более широкий смысл проверки на значимость. Конечно, она является средством получения валидных выводов об экспериментальной гипотезе, но это еще далеко не все. Главная тема настоящей главы — значимые результаты — выходит далеко за пределы технического вопроса о статистической значимости.
Мы собираемся изложить в этой главе вопросы о статистических выводах несколько нетрадиционным способом — без уравнений или вычислений. Последние можно найти, как и в предыдущих главах, в статистическом приложении. Таким образом, вы не сможете сами проводить проверку статистической значимости до тех пор, пока не познакомитесь с этим приложением. Однако те идеи, которые важны для экспериментаторов, рассматриваются достаточно детально. Если вы разберетесь в них, это поможет вам при чтении экспериментальных статей, поскольку вы сможете увидеть, как авторами были сделаны заключения. Вы узнаете, какие статистические решения можно сделать относительно нуль-гипотезы и как они относятся к экспериментальным выводам. Возможно даже, что вы не согласитесь с каким-нибудь исследователем либо в связи с использованным правилом статистического решения, либо в связи с выводом, сделанным на основе применения этого правила.
Основные темы, по которым вам будут заданы вопросы в конце главы, следующие:
1. Как проверяется нуль-гипотеза?
2. Виды риска при принятии статистического решения.
3. Как проверка нуль-гипотезы связана с внутренней валидностью?
4. Как этот вид валидности входит в более общую картину экспериментальной валидности?
НУЛЬ-ГИПОТЕЗА
Кажется весьма странным проверять нуль-гипотезу о том, что интенсивность плача не различается в случаях, когда комнату покидает мать и когда уходит ассистентка. Ведь это противоречит тому, что предполагает экспериментатор. Экспериментальная гипотеза состоит как раз в том, что плач сильнее, когда уходит мать.
Существуют два основания для такого «хода от противного». Первое состоит в том, что любой реальный эксперимент (который не является ни идеальным, ни бесконечным) не может быть абсолютно доказательным. Мы никогда не сможем сказать, что безусловно и навсегда доказали, что наши условия различные. Мы не в состоянии «доказать» экспериментальную гипотезу. Самое большее, что мы можем сделать, — это показать, что альтернативные объяснения неправильны, чтоприводит нас ко второму основанию обращения к нуль-гипотезе. Это специфическая гипотеза, и ее отвержение имеет большой смысл. Так как она специфическая (разница между условиями равна нулю) в отличие от экспериментальной гипотезы (для одного условия показатель больше), она доступна стандартной статистической проверке. Это и составляет ее смысл. Ведь если неверно, что данные условия не различаются, значит, мы точно знаем, что они в чем-то различны.
Третье возможное заключение
Очевидно, вам было не очень приятно узнать из 2-й главы, что в любом эксперименте приходится делать одно из двух конкурирующих заключений: 1) подтверждена экспериментальная гипотеза о том, что зависимая переменная имеет более высокое значение для условия А, чем для условия Б; 2) подтверждена противоположная гипотеза о большем значении зависимой переменной для условия Б, чем для условия А. (Наверное, все это больше огорчает вашего преподавателя.) Что же тогда можно сказать о выводе, что ни одна из конкурирующих гипотез не подтвердилась? Вообще говоря, мы не должны заботиться об этом третьем возможном заключении при использовании результатов таких простых экспериментов, которые описаны в начале книги. Ткачиха может либо носить наушники, либо нет. Она не выберет компромиссного решения носить только один из них, если разница в пользу наушников окажется очень незначительной. Если нет проблемы стоимости или удобства, почему бы не принять к сведению любую полученную разницу, как бы мала она ни была? Всегда есть некоторая вероятность того, что условие, обнаруживающее преимущество в эксперименте, сохранит его и в будущем. Другими словами, в случае таких простых практических решений правило состоит в том, чтобы учитывать любые позитивные данные. Тогда в процессе решения для третьего заключения не остается места.
Однако в экспериментах, подобных описанному в предыдущей главе, где ложное заключение нанесет ущерб научному знанию, необходимо рассматривать третье возможное заключение, состоящее в том, что независимая переменная оказалась просто неэффективной. Итак, на основании результатов эксперимента Фли-нера и Кернса можно было сделать три заключения, каждое из которых относится к тому, что могло бы быть получено в бесконечном или идеальном эксперименте:
1. Подтвердилась гипотеза, что дети данной возрастной группы плачут больше, если уходит мать.
2. Подтвердилась гипотеза, что дети плачут больше, если уходит ассистентка.
3. Ни одна из приведенных гипотез не подтвердилась.
Указанные исследователи понимали, что в любом реальном ограниченном эксперименте как положительные результаты (плач сильнее, когда уходит мать), так и отрицательные результаты (плач сильнее, когда уходит ассистентка) могут быть чисто случайными. Поэтому только достаточно большое различие в интенсивности плача при уходе матери по сравнению с уходом ассистентки могло бы рассматриваться как подтверждение экспериментальной гипотезы о том, что то же самое обнаружится в идеальном или бесконечном эксперименте. Меньшее различие имело бы весьма высокую вероятность оказаться случайным.
Мы можем представить связь между полученным различием и заключением, сделанные на его основе при помощи следующей диаграммы:
Заключение — результаты подтверждают:
| Противоположную гипотезу: плач сильнее, если уходит ассистентка | Ни одну из гипотез | Экспериментальную гипотезу: плач сильнее, если уходит мать | ||||||||
| -5 | -4 | -3 | -2 | -1 | 0 | +1 | +2 | +3 | +4 | +5 |
Интенсивность плача при уходе матери минус интенсивность плача при уходе ассистентки
Тонкая вертикальная черточка над значением +3,40 справа показывает, что это различие (для старшей группы) было достаточно для подтверждения экспериментальной гипотезы, что плач сильнее, если уходит мать. С другой стороны, вертикальная отметка над значением +0,93 (различие для более младшей группы) показывает, что это различие недостаточно для подтверждения экспериментальной гипотезы. Для того чтобы подтверждалась либо экспериментальная гипотеза, либо противоположная гипотеза, требуется различие порядка ±3 единицы.
Отвержение или неотвержение нуль-гипотезы
Правило статистического решения. Три рассмотренных выше возможных заключения из результатов эксперимента делаются на основе правила статистического решения. Здесь оно состояло в том, что нуль-гипотеза может быть отвергнута только в случае, если вероятность получения различия, удовлетворяющего нуль-гипотезе, меньше, чем 0,05 (т. е. меньше 1 из 20).
Основа статистического вывода. Если бы Флинер и Кернс многократно повторяли свой эксперимент на новых группах детей той же возрастной категории, они бы не получали в каждом эксперименте разницу между средними для ухода матери и для ухода ассистентки, в точности равную 3,40. Из-за случайных вариаций эта разница была бы то больше, то меньше. Если бы для бесконечного числа повторений общая средняя разница равнялась в точности 0, это означало бы справедливость нуль-гипотезы. Однако для каждого отдельного эксперимента можно было бы ожидать значение, отличное от нуля.
Итак, разность «мать — ассистент» будет варьировать от эксперимента к эксперименту. Величина разброса этих разностей зависит от надежности каждого эксперимента. Как мы видели в главе 2, надежность выше и, следовательно, разброс от эксперимента к эксперименту меньше, чем больше число наблюдений и чем меньше случайных вариаций. Поэтому разброс разностей «мать — ассистент» был бы меньше, если бы каждый эксперимент проводился на большом числе испытуемых и имел небольшое стандартное отклонение.
Из числа испытуемых и стандартного отклонения можно вывести величину различия, которая при справедливости нуль-гипотезы может быть превышена лишь с вероятностью 0,05. Нахождение этой величины назы вается статистическим выводом. Такая величина для эксперимента Флинера и Кернса оказалась порядка ±3. (Она была определена с помощью статистической процедуры нахождения так называемого t-критерия. Описание ее можно найти в статистическом приложении к данной главе. Это один из многих критериев статистической значимости, используемых экспериментаторами.)
Диаграмма на с. 241 показывает, как в эксперименте Флинера и Кернса применялось правило статистического решения для получения одного из трех возможных выводов.
Как видно, различие +3,40 для старших детей попадает в одну из двух областей отвержения нуль-гипотезы. Если бы нуль-гипотеза была верна, только 0,05 части всех экспериментов дала бы различия, попадающие в ту или другую область отвержения. Для данного эксперимента вероятность (р) для каждой области отвержения будет 0,025 и для области «неотвержения» нуль-гипотезы — 0,95. Используя правило решения 0,05, мы говорим, что полученное различие значимо, поскольку мы можем отвергнуть нуль-гипотезу. Меньшее различие +0,93, как это видно, не попадает в область отвержения. Следовательно, статистическое решение в этом случае состоит в том, чтобы не отвергать нуль-гипотезу. Этот результат мог бы быть получен с вероятностью более высокой, чем 0,05, если бы нуль-гипотеза была верна.
Итак, мы можем заключить, что старшие дети. плачут сильнее, если уходит мать. Что касается младшей группы, то мы не можем сделать ни этого, ни противоположного вывода (что они плачут сильнее с уходом ассистентки).
Заключение — результаты подтверждают:
| Противоположную гипотезу: плач сильнее, если уходит ассистентка | Ни одну из гипотез | Экспериментальную гипотезу: плач сильнее, если уходит мать | ||||||||
| -5 | -4 | -3 | -2 | -1 | 0 | +1 | +2 | +3 | +4 | +5 |
Статистическое решение:
| Отвергнуть нуль-гипотезу (р = 0,025) | Не отвергать нуль-гипотезу (p = 0,95) | Отвергнуть нуль-гипотезу (р = 0,025) | ||||||||
| -5 | -4 | -3 | -2 | -1 | 0 | +1 | +2 | +3 | +4 | +5 |
Интенсивность плача при уходе матери минус интенсивность плача при уходе ассистентки
Факторы, влияющие на величину требуемого различия
Предыдущая диаграмма продемонстрировала величину различия между средними, необходимую для отвержения нуль-гипотезы в условиях частного конкретного набора данных. При более надежных данных для отвержения нуль-гипотезы оказывается достаточным меньшее различие. Однако если для отвержения нуль-гипотезы используется более строгий критерий, то необходимо большее различие между средними. Эти два фактора иллюстрируются на рис. 6.1.
Влияние надежности. Если бы увеличили число обследованных детей или стандартное отклонение внутри каждой группы оказалось меньше, то надежность увеличилась бы. Это означает, что в наборе бесконечно повторяемых экспериментов средние значения варьировали бы меньше. А в таком случае варьировали бы меньше и различия между средними. Вокруг каждой общей средней было бы более плотное распределение. В результате при справедливости нуль-гипотезы две линии, показывающие на диаграмме, куда попадает (с плюсом или с минусом) 0,025 части всех реальных средних, должны оказаться ближе кнулю.
На рис. 6.1 верхняя диаграмма (а) уже была представлена; на ней показаны результаты обследования 15 детей. На средней диаграмме (б) линиями показаны области отвержения нуль-гипотезы при условии, что число детей было увеличено до 60 или что стандартное отклонение для каждой пробы было уменьшено наполовину. И в том и в другом случае требуемое различие уменьшается вдвое, примерно до ±1,5. Видно, что различие 0,93, обнаруженное в младшей группе, тем не
|
|
| Рис. 6.1. Исходное статистическое решение (а), результат повышения надежности (б) и величина различия, необходимая для отвержения нуль-гипотезы (в). На числовых осях: интенсивность плача после ухода матери минус интенсивность плача после ухода ассистентки |
менее остается вне области отвержения нулевой гипотезы, что опять не дает возможность подтвердить гипотезу о том, что ребенок больше плачет при уходе матери. Тем не менее если бы выборка была увеличена еще больше или стандартное отклонение оказалось меньше, различие 0,93 (если бы оно, конечно, было получено) оказалось бы значимым. Сложность в том, что при более надежных данных было бы менее вероятно получить различие такого уровня, если нулевая гипотеза была верна.
Влияние правила решения. До сих пор фигурировало только одно правило решения: нуль-гипотеза отвергается, если вероятность получения различия, при котором нуль-гипотеза верна, меньше 0,05. Вероятность, используемая для отвержения нуль-гипотезы, называется альфа-уровнем. Если применяется более строгий критерий, это означает, что нуль-гипотеза отвергается, если подтверждающая ее разница встречается в меньшей доле случаев. Наиболее часто это 0,01 (1 эксперимент из 100) вместо 0,05 (1 из 20).
Результат использования в правиле решения альфа-уровня 0,01 вместо прежнего 0,05 виден на нижней диаграмме (в) рис. 6.1. (Первоначальная выборка из 15 детей и первоначальные стандартные отклонения здесь сохранены.) При альфа-уровне 0,01 для отвержения нуль-гипотезы требуется различие, большее ±4. При этом, более строгом критерии уже нельзя сделать заключение в пользу гипотезы о более сильном плаче с уходом матери.
Способ, каким в большинстве статей сообщается о статистически значимом различии, выглядит так: «p̄<0,05» или «р<0,01». Это означает, что вероятность случаев, когда нуль-гипотеза верна, меньше 0,05 или меньше 0,01. Незначимое различие представляется как «р>0,05» или «р>0,01».
ОТ РЕШЕНИЙ К ВЫВОДАМ
Люди, которые не любят статистику, считают, что все эти модные проверки статистической значимости не имеют особого смысла. Они не правы. С другой стороны, люди, поклоняющиеся статистике, считают, что за каждым статистическим решением автоматически следует экспериментальный вывод. Они тоже не правы. Мы попытаемся показать, что истина находится между этими крайностями. Наш девиз: используйте статистику, но сделайте так, чтобы она стала вашей служанкой, а не вашей госпожой.
Игнорирование проверки на значимость
Предположим, что Флинер и Кернс не стали бы рассматривать нуль-гипотезу. Они решили бы расценивать любое различие в пользу ухода матери как подтверждающее их экспериментальную гипотезу. В таком случае они приняли бы различие 0,93 для младшей группы тоже как значимое. Это было бы довольно рискованно. При дальнейшем знакомстве с их статьей можно увидеть, что для самой младшей исследовавшейся группы детей (в возрасте от трех до пяти месяцев) различие оказалось равным 1,78 с противоположным знаком, т. е. плач был больше при уходе ассистентки. Таким образом, выбирая тактику постоянного игнорирования нуль-гипотезы, экспериментаторы вынуждены были бы прийти к подтверждению противоположной гипотезы, которая в данном случае выглядит довольно бессмысленно.
Мы можем сразу увидеть, к каким последствиям приведет противоположная тактика, при которой нуль-гипотеза никогда не отвергается. Польза от проверки нуль-гипотезы всегда видна сразу. Если куль-гипотеза окажется верной, экспериментальные выводы, не учитывающие ее, всегда будут ложными: будет считаться, что получила подтверждение либо экспериментальная гипотеза, либо противоположная ей гипотеза. Более того, когда нуль-гипотеза неверна и существует некоторое действительное различие в пользу того или иного условия, выводы тоже зачастую могут оказаться ложными. Предположим, что для младших детей бесконечный эксперимент показал небольшое преобладание плача при уходе матери. В любом конкретном эксперименте это различие вполне могло оказаться с противоположным знаком. Эта последняя ошибка будет делаться тем чаще, чем меньше надежность данных. Вообще говоря, в младшую группу входило только девять детей, так что надежность полученных по ним данных довольно сомнительна.
Итак, в научных экспериментах мы не можем обойтись без проверки на значимость.
Разновидности риска и типы ошибок
Поскольку нам известно, что реальные эксперименты не бывают ни идеальными, ни бесконечными, мы знаем, что некоторые из наших решений окажутся ошибочными независимо от применявшегося правила решения. Может быть, Флинер и Кернс не следовало отвергать нуль-гипотезу для старшей группы. Может быть, нуль-гипотеза была верна. Если бы они использовали 0,01 альфа-уровень, они не смогли бы отвергнуть нуль-гипотезу. И было бы прекрасно, если бы нуль-гипотеза и в самом деле была правильной. Ну а что, если нет? При обоих альфа-уровнях они рисковали бы — но противоположным образом.
Ошибки I типа. Первый риск состоит в возможности ошибки I типа: отвержение нуль-гипотезы, когда она верна. Если исследователь использует в правиле решения уровень 0,05, это означает, что он готов сделать такую ошибку не более чем в пяти процентах его экспериментов. Когда он затем принимает отвержение нуль-гипотезы в качестве подтверждения экспериментальной гипотезы (например плач более сильный при уходе матери), это показывает его чрезмерный оптимизм. Ведь существует 1 шанс из 20, что такое доказательство ошибочно.
В любом эксперименте, направленном на проверку совершенно новой гипотезы, противоречащей общепринятому представлению, можно посоветовать быть более осторожным. Ломать научные традиции — вещь очень серьезная, и для этого нужно быть абсолютно уверенным в своих фактах. В таких случаях рекомендуется использовать более строгое правило решения, с 0,01 альфа-уровнем. Наука еще может выдержать 1 процент результатов, которые ошибочно приняты за подтверждающие экспериментальную гипотезу, но 5 процентов — это уж слишком!
Ошибки II типа. Если мы настаиваем на 0,01 альфа-уровне (или даже более строгом уровне, таком, как 0,001), появляется новый риск: наше желание быть абсолютно уверенными может привести нас к ошибочному неотвержению нуль-гипотезы, когда она на самом деле неверна. Вполне естественно, что это называют ошибкой II типа. Если нуль-гипотеза ошибочна, верна должна быть какая-то другая гипотеза. Риск не отвергнуть нуль-гипотезу, когда верна другая гипотеза (например определенное различие в плаче при уходе матери и ассистента), может быть также выражен через вероятность, называемую бета-уровнем.
Для данной совокупности экспериментальных результатов уменьшение альфа-уровня означает увеличение бета-вероятности для любой ненулевой гипотезы. Использование очень строгого правила решения означает, что экспериментатор готов пойти на значительный риск, заключающийся в неотвержении нулевой гипотезы, когда верна какая-то другая гипотеза. Таким образом, при низком альфа-уровне экспериментатор будет часто ошибочно заключать, что результаты не подтверждают экспериментальную гипотезу. В отличие от альфа-уровня, для бета-уровня невозможно задать некоторое общее значение вероятности; она различается для каждой конкретной ненулевой гипотезы о различии между условиями. Так, если окажется верной гипотеза о большом различии между условиями (скажем, разница в интенсивности плача +5 ед.), вероятность не отвергнуть нуль-гипотезу (бета) будет низкой даже при использовании строгого альфа-уровня 0,01. С другой стороны, если действительная разность окажется небольшой (скажем, + 1,0), вероятность ошибочного решения не отвергнуть нуль-гипотезу будет намного больше. Однако, логика отношений сохраняется: при одних и тех же данных уменьшение альфа-уровня увеличивает бета-вероятность для всех статистических гипотез, отличных от нуль-гипотезы.
О статистической проверке экспериментальных результатов говорят как об имеющей силу в той степени, в какой бета-величина остается низкой для ненулевых гипотез. При хорошей силе выявляются реальные различия. Конечно, сила автоматически повышается с использованием нестрогого правила решения (например 0,10 альфа-уровня), но это увеличивает риск ошибки I типа. Существует два более удачных способа увеличения силы. Один состоит в увеличении надежности данных. Как мы видели на рис. 6.1 (в), даже при небольшом различии между условиями оказывается возможным отвергнуть нуль-гипотезу либо путем увеличения числа испытуемых, либо путем уменьшения случайных вариаций. Другой способ состоит в использовании наиболее эффективных экспериментальных схем и проверок. Те и другие описаны в специальной литературе (см., например, Коэн, 1977).
В предыдущем параграфе уже говорилось, что ошибки I типа следует избегать в том случае, когда отвержение нуль-гипотезы связано с отрицанием существующих идей или результатов предыдущих экспериментов. С другой стороны, если экспериментатор не обнаруживает значимых различий между условиями, которые обычно признаются эффективными, это его заключение должно основываться на использовании высокого (или нестрогого) альфа-уровня, чтобы уменьшить риск ошибки II типа. Почти любой полученный ранее правильный результат может быть «опровергнут» путем ошибочного неотвержения нуль-гипотезы: либо через использование ненадежных данных, либо через применение слишком строгого правила решения, либо (самый худший вариант) через то и другое вместе.
Теперь давайте рассмотрим, какие выводы должен сделать экспериментатор при отвержении нуль-гипотезы.
Заключения при неотвержении нуль-гипотезы. Пожалуйста, заметьте: в отношении нуль-гипотезы принимается только два статистических решения — отвергнуть ее или не отвергнуть. Никогда не бывает решения принять нуль-гипотезу. Все же для экспериментатора иногда полезно заключить, что независимая переменная не оказывает никакого влияния. Как видно из диаграммы на с. 241, неотвержение нуль-гипотезы привело бы к заключению, что не подтверждается ни экспериментальная гипотеза, ни противоположная ей гипотеза. Например, для младшей группы детей небольшое различие в интенсивности плача не благоприятствует ни гипотезе о более сильном плаче при уходе матери, ни противоположной гипотезе о более сильном плаче при уходе ассистентки. Однако из подобных неподтверждений можно вывести различные заключения.
Во-первых, экспериментатор может сделать вывод, что он не знает, оказывает ли независимая переменная вообще какое-либо влияние на поведение. Этот вывод особенно подходит к случаю, когда надежность низка из-за небольшого количества испытуемых или из-за большей, чем ожидалось, вариабельности поведения. Так, Флинер и Кернс могли бы решить продолжить эксперимент на новых детях, относящихся к той же младшей группе, и попытаться уменьшить случайные вариации, насколько это возможно.
Во-вторых, экспериментатор может заключить, что надежность была вполне удовлетворительной и что неотвержение нуль-гипотезы означает, что исследовавшиеся условия действительно не различаются. Это заключение может оказаться наиболее справедливым, особенно если более ранние эксперименты показали неэффективность независимой переменной.
Итак, статистическое решение снова состоит в неотвержении нуль-гипотезы. Однако обстоятельства эксперимента заставляют сделать вывод, что независимая переменная оказалась недейственной.
Валидность выводов
Вернемся к определению внутренней валидности, данному в главе 2: это степень уверенности, что заключение об экспериментальной гипотезе совпадает с выводом, который был бы получен в идеальном или бесконечном эксперименте. В предыдущих главах мы видели, как увеличивается внутренняя валидность е помощью процедур, повышающих надежность данных и уменьшающих смешение. Понятно, что заключения из экспериментальных данных не могут быть лучше самих данных. В настоящей главе мы видели, как разумное использование правил статистического решения ведет к обоснованным заключениям об экспериментальной гипотезе. Это — тоже способ увеличения внутренней валидности, поскольку заключение составляет наиболее важную часть эксперимента. Остановимся на этом более подробно.
Бесконечный эксперимент одновременно и определяет полную внутреннюю валидность, и обеспечивает основу для проверки нуль-гипотезы. Конечно, для этой последней цели существует особый вид бесконечного эксперимента. Он разбивается на отдельные конкретные эксперименты. Каждый из них такой же, как и реально проводимый эксперимент, но только в каждом эксперименте берутся другие испытуемые, выбранные из той же популяции (или другие пробы, если мы обращаемся к интраиндивидуальной схеме эксперимента).
При проверке нуль-гипотезы мы должны предположить, что из бесконечного эксперимента, безусловно, следует заключение, что экспериментальные условия не различаются. Естественно, общая средняя разность между условиями по всем этим экспериментам должна равняться нулю. Однако для каждого отдельного эксперимента это будет не так. Разности между средними будут лишь распределяться вокруг нуля, но при этом некоторые эксперименты будут благоприятствовать одному условию, другие — другому. А теперь нам нужно соотнести различие, полученное в нашем собственном эксперименте, со всем набором различий, которые могли бы быть получены в этом типе бесконечного эксперимента.
Достоверные заключения, когда нуль-гипотеза верна. Если оказалось, что нуль-гипотеза верна, т. е. если общая средняя разность между условиями в бесконечном эксперименте равна нулю, мы хотели бы иметь возможность прийти к такому же заключению и в нашем эксперименте. Ведь мы не хотим заключить в пользу гипотезы о различии между условиями, если много шансов за то, что на основе бесконечного эксперимента мы пришли бы к выводу об отсутствии различия. Таким образом, из надежных данных мы сделаем вывод, что экспериментальная гипотеза о различии условий неверна, если разность такой величины, как в нашем эксперименте, при верности нуль-гипотезы может появиться с вероятностью 0,05 или 0,01. Мы хотели бы быть уверенными в таком заключении при проверке новой экспериментальной гипотезы, особенно если она идет вразрез с общепринятым убеждением. Вот почему в таком случае альфа-уровень должен быть 0,01 или ниже. При уровне 0,05—5 процентов заключений будут неверны. В бесконечном числе экспериментов 5 процентов дали бы результаты, которые привели бы к отвержению нуль-гипотезы в единичном эксперименте.
Достоверные выводы, когда нуль-гипотеза неверна. Если нуль-гипотеза оказывается ложной, т. е. если общая средняя разность между условиями такова, как предсказывает экспериментальная гипотеза, хотелось бы прийти к такому же выводу и в нашем эксперименте. Это не так важно при проверке какой-то новой идеи. Если она верна, то ее время все равно придет. Однако если различие между условиями ожидается на основе уже имеющихся знаний, мы хотим быть совершенно уверенными в своем выводе в пользу экспериментальной гипотезы.
Как мы уже видели, для этого требуются надежные данные. Кроме того, необходимо использовать менее строгое правило решения, например альфа-уровень 0,05. Если нуль-гипотеза окажется верной, мы, конечно, хотели бы сделать именно такое заключение. Однако мы готовы увеличить риск ошибочного отвержения нуль-гипотезы для того, чтобы уменьшить риск ошибочного вывода об отсутствии различия между условиями, т. е. в ситуации, когда бесконечный эксперимент такие различия бы показал.
НЕПРИЯТНЫЕ ПРОБЛЕМЫ, КОТОРЫЕ ОСТАЮТСЯ
Экспериментатор может благополучно пройти в своих заключениях через минное поле рисков относительно нуль-гипотезы и все же не внести никакого вклада в научное знание. В данном разделе рассматриваются три «трудные проблемы», которые угрожают внутренней валидности заключений, сделанных на основе правил решения, несмотря на то что данные надежны и проверка значимости осуществлена весьма разумно.
Бросающиеся и не бросающиеся в глаза результаты
Один исследователь предложил в шутку использовать для определения значимости результатов своего рода «интерокулярный травмирующий тест». Согласно этому «тесту» понять, что означают полученные результаты, можно, только если вывод «бьет вас прямо в переносицу» (Дж. Берксон, цит. по: Эдвардс, Линдман и Сэвеж, 1963). Конечно, он имел в виду эксперимент, в котором ожидается сильный эффект, большое различие между условиями.
В отношении действия независимой переменной обычно имеется одно из двух ожиданий. Первое — что исследуемое поведение сильно зависит от переменной и что присутствие или отсутствие последней повлечет за собой большие различия. Так, мы могли бы ожидать, что человек с закрытыми глазами будет хорошо локализовать звук только в том случае, если звуки, достигающие обоих ушей, будут физически различаться. Если же его оценки будут успешны и без подобного различия, значит, независимая переменная не настолько важна, как предполагалось. Экспериментальная гипотеза, таким образом, не подтвердилась бы, даже если бы нулевая гипотеза была отвергнута.
Второе, иногда все, что имеет смысл ожидать от разных условий, — это небольшое, но стойкое различие. Рассмотрим эксперимент на перцептивную защиту, которая, 252как предполагают, обнаруживается в том, что нецензурные слова, предъявленные на короткое время, плохо опознаются. Различие в количестве опознанных нецензурных и нейтральных слов (какова бы ни была причина его) не будет предполагаться большим: ожидаемое влияние 6удет почти забито другими факторами. Например, некоторые нейтральные слова могут быть неточно восприняты или воспроизведены из-за смешения с другими словами. Некоторые из «нейтральных» слов также могут относиться к неприятным ситуациям в прошлом данного человека. Наконец, колебания внимания во время эксперимента могут влиять на опознание слов возможно даже больше, чем вариации в «пристойности». При таком ожидании незначительная, но постоянная тенденция к худшему опознанию неприличных слов была бы уже достаточной для демонстрации действия независимой переменной.
Эксперимент Флинера и Кернса был как раз таким, в котором можно было ожидать не бросающийся в глаза результат. Хотя ребенок, естественно, привязан к матери и поэтому очевидно, что с уходом матери он будет плакать сильнее, этот эффект вполне может затушеваться другими факторами. Возможно, например, что некоторые матери из-за занятости на работе проводят со своими детьми сравнительно мало времени, и поэтому привязанность детей к ним не столь велика. Другие матери ведут себя так, что приходят и уходят на глазах у ребенка по многу раз в день, приучая его к своему отсутствию. Ассистенты по внешнему виду и манере поведения могут оказаться похожими на мать в большей или меньшей степени. Далее Флинер и Кернс (1970, с. 218) обнаружили, что некоторые дети вообще плачут почти все время в течение эксперимента: «Пожалуй, наиболее очевидной чертой плача было его постоянство: если ребенок начинал сильно плакать, он скорее всего продолжал это делать и дальше». Все эти факторы могли затруднить выявление различия между уходом матери и уходом ассистентки. Таким образом, данный эксперимент относится к тем, в которых нельзя ожидать отчетливого результата. Действие переменной — уход определенною лица — может быть выявлено 253лишь через статистическое различие в интенсивности плача. И здесь нельзя требовать такого различия, которое «бьет в глаза».
Количество не помогает
По мере значительного увеличения числа испытуемых с целью увеличения силы проверки на значимость происходит любопытная вещь. Оказывается, что любые два условия начинают давать статистически значимые различия (Бакан, 1967). Если значимость не будет обнаружена для 20 испытуемых, она появится для 200, или 2 000, или 2 000 000. В этом нет никакой мистики. Любые два сравниваемых условия включают много факторов, помимо тех, которые они должны представлять. Мы уже говорили, что человек не в силах контролировать все привходящие обстоятельства. Возможно, что буквы распознаются лучше, чем числа, только потому, что в каждой тысяче находится несколько испытуемых, которые реагируют отрицательно на числа в силу неудачного опыта в школьной математике. Возможно, что слова, произносимые каждые 8 секунд, воспринимаются хуже, чем произносимые в другом темпе, поскольку они немного чаще совпадают с обычными глотательными движениями, уменьшающими способность слышать.
Такие дополнительные факторы обнаруживают всегда свое присутствие при анализе больших массивов данных. Наш основной урок состоит в том, чтобы не позволять себе слишком зависеть от тестов на значимость в заключениях об исследуемых факторах. Ведь это только одно из средств. С особенной осторожностью следует подходить к случаям, которые требуют для выявления действия независимой переменной слишком большого количества данных. Гораздо большее впечатление производят статистически значимые различия, полученные на относительно небольшом числе испытуемых или проб.
Справедлив ли вывод для всех испытуемых !
Флинер и Кернс вполне могли бы получить статистически значимые результаты для детей старшей группы, если бы только девять из пятнадцати детей плакали сильнее при уходе матери. Но что в таком случае сказали бы об остальных шести?
Проводя эксперимент, мы рассчитываем, что исследуемый психологический фактор действует эффективно на каждого испытуемого. Читая статьи в журналах, вы обнаружите, что это положение принимается почти всеми. Негласное допущение состоит в том, что если независимая переменная эффективна, она влияет на всех индивидов, подпадающих под данную гипотезу. Если последняя в самом деле верна для некоторых, она верна для всех. Поэтому отсутствие в шести случаях более сильного плача при уходе матери приписывается действию дополнительных факторов, о которых упоминалось выше: прошлому опыту в общении с матерью, предшествующему плачу в эксперименте и т. д.
Однако это не всегда так. Рассмотрим другой эксперимент. Предположим, обнаружено, что испытуемые лучше узнают слова, если они проговаривают их вслух при первом предъявлении. По крайней мере, 13 из 20 испытуемых показали именно этот результат. Тогда причиной, по которой тот же результат не наблюдался у других семи испытуемых, могут быть случайные вариации, связанные, например, с ассоциациями, которые вызывали некоторые из использовавшихся слов. Однако могло оказаться, что одни испытуемые помогали себе немедленным проговариванием, а другие — нет. Проводя индивидуальные эксперименты, можно было бы выявить реальные причины индивидуальных различий каждого испытуемого. Еще лучше, если нам удастся найти некоторые признаки, разделяющие лиц, которым проговаривание помогает и которым — нет. Вполне возможно, например, что проговаривание не помогает лицам с очень хорошей визуализацией. Но мы забегаем вперед, поднимая вопрос, который будет рассматриваться в главе 8, где мы будем свидетелями рождения еще одного или даже двух новых способов контроля.
ДРУГИЕ АСПЕКТЫ ВАЛИДНОСТИ
В этой главе мы говорили о заключениях, основанных на статистических решениях. Однако мы не должны упускать из виду, что существуют и другие важные аспекты валидности. Слишком часто о валидности заключения судят, лишь учитывая надежность, которой, мы занимались в данной главе. Но мы, конечно, знаем,, что валидность этим не исчерпывается.
Внешняя валидность
Напомним прежде всего, что эксперимент может не обладать внешней валидностью по ряду причин. Эксперимент может не быть экспериментом полного соответствия из-за несоответствующего уровня другой переменной (например если бы Джек Моцарт запоминал, вальсы вместо сонат при сравнительной оценке методов заучивания). В экспериментах, которые улучшают реальный мир (например с ночными посадками самолетов), мы хотим также быть уверенными, что искусственные независимая и зависимая переменные представляют те ситуации, к которым затем будут прилагаться результаты. В экспериментах, проводимых на выборке испытуемых (с информацией о стоимости товаров), мы рассматривали вопрос, насколько хороша данная выборка представляет популяцию покупателей универсама. Анализируя конкретные способы представления экспериментальной ситуации различных схем социальной структуры (авторитарной, демократической или анархистской), мы больше всего сомневались относительно операциональной валидности этих ситуаций.. Все наши статистические решения имеют отношение к внешней валидности. Тем не менее экспериментальные выводы не могут быть до конца валидными, если они наряду с внутренней валидностью не будут обладать внешней валидностью.
Систематическое смешение
Напомним далее о рассматривавшейся в главе 2 необходимости избегать систематического процедурного смешения (такого, как эффекты последовательности) и в главе 5 — сопутствующего смешения. Мы видели, что Флинер и Кернс (1970) сделали вывод о более сильном плаче при уходе матери, чем при уходе ассистентки. Однако, как показалКоэн (1977), здесь имело место систематическое сопутствующее смешение. Ведь остававшийся человек был разным, когда уходила мать и когда уходила ассистентка. Тем самым ложится тень на внутреннюю валидность независимо от величины различия между двумя условиями. Отвержение нулевой гипотезы ничего не говорит о систематическом смешении. Экспериментальные заключения могут иметь внутреннюю валидность лишь в той степени, в какой удалось избежать систематического смешения.
Когда мы судим о валидности экспериментальных заключений на основе статистических решений (хорошо или плохо они были использованы или они вообще были неверно проигнорированы), мы должны предполагать, что все ранее рассмотренные аспекты валидности удовлетворительно реализованы. Вам следует об этом хорошо помнить или еще лучше — «зарубить себе на носу».
КРАТКОЕ ИЗЛОЖЕНИЕ
Большие различия в действии разных условий независимой переменной приводят экспериментатора к выводу о подтверждении экспериментальной гипотезы. Меньшие различия интерпретируются как случайный результат. Основанием для таких различных выводов является статистическая значимость. Более конкретно это означает, что если бы в идеальном или бесконечном эксперименте различие отсутствовало, то было бы мало вероятно получить в конкретном эксперименте большое различие, не так невероятно — меньшее различие.
В научных экспериментах — в отличие от тех, где существует только два практических исхода — возможны три заключения из экспериментальных данных. В дополнение к подтверждению экспериментальной 257или противоположной ей гипотезы возможно заключение о не подтверждении ни одной из них. Какое именно из этих трех заключений будет сделано, зависит от статистического решения относительно нуль-гипотезы.
Если бы был проведен бесконечный эксперимент и нуль-гипотеза оказалась верной, то среднее различие между условиями было бы равно нулю. Однако в отдельных конкретных экспериментах различия могут быть как в пользу одного условия, так и в пользу другого. Если различие настолько велико, что очень редко могло бы быть получено в бесконечном эксперименте, нуль-гипотеза отвергается. Однако если вероятность появления различия, подобного полученному, достаточно высока, нуль-гипотеза не отвергается. Когда нуль-гипотеза отвергается, делается вывод о подтверждении экспериментальной гипотезы (или противоположной ей гипотезы, если различие оказалось с обратным знаком). Когда нуль-гипотеза не отвергается, ни экспериментальная, ни противоположная ей гипотезы не подтверждаются. Это последнее заключение может означать одно из двух. Если данные ненадежны, заключение будет состоять в том, что действие независимой переменной просто не удалось выявить. При надежных данных экспериментатор может быть уверен, что условия не оказывают различного действия.
Величина различия между условиями, необходимая для отвержения нуль-гипотезы, определяется двумя факторами. Первое — это надежность. Чем больше надежность, тем меньше различие, допускающее отвержение. Второй фактор — вероятность того, что экспериментатор рискнет ошибочно отвергнуть нуль-гипотезу, когда она верна. Он называется альфа-уровнем правила его решения. Ошибка, которая будет увеличиваться с возрастанием этого риска, называется ошибкой I типа. Так, риск ошибки I типа в пять раз выше при альфа-уровне 0,05 по сравнению с альфа-уровнем 0,01.
Однако при уменьшении альфа-уровня увеличивается риск противоположной ошибки. Это риск не отвергнуть нуль-гипотезу, когда верна некоторая другая гипотеза (и, конечно, нуль-гипотеза ошибочна). Это называют ошибкой II типа. Для любого конкретного набора данных эта вероятность (называемая бетой) увеличивается с уменьшением альфа-уровня. Однако, увеличивая надежность эксперимента, можно найти приемлемую величину бета даже при строгом альфа-уровне. Говорят, что статистическая проверка имеет силу в той мере, в какой низка вероятность бета и в которой может быть выявлено истинное различие.
Использование строгого альфа-уровня (например, 0,01) рекомендуется в тех случаях, когда различие между условиями должно подтвердить новую гипотезу, противоречащую общепринятому мнению. Эта строгость нужна для того, чтобы не засорять науку слишком большим числом артефактов. 5 ложных утверждений из 20 — это слишком тяжелое бремя для науки. С другой стороны, если результаты показали влияние независимой переменной, его нельзя сбрасывать со счетов только потому, что различие не достигло уровня значимости 0,01.
Назначение проверок на значимость — повышение внутренней валидности. Ведь внутренняя валидность и проверка нуль-гипотезы 258могут быть описаны через бесконечный эксперимент. В бесконечном эксперименте, состоящем из множества отдельных экспериментов (таких, какие проводятся реально), общее среднее различие между условиями будет равно нулю, если верна нуль-гипотеза. Однако различия, обнаруживаемые в отдельных экспериментах, не будут равны нулю, а лишь только распределятся вокруг нуля. Экспериментатор может выяснить это распределение. Он соотнесет полученное различие с его вариабельностью, но не будет делать вывода о различии только на том основании, что много отдельных экспериментов дает достаточно большое различие.
Если же верна нуль-гипотеза, экспериментатор также хотел бы обосновать и этот вывод. Но даже чтобы иметь возможность сделать вывод о правильности какой-то другой гипотезы, экспериментатор вынужден идти на некоторый риск. Экспериментатор хочет иметь заключение о верности экспериментальной гипотезы с такой степенью обоснованности, как если бы ожидаемое различие было получено в бесконечном эксперименте. Положение, которое он в конце концов занимает между ошибками I и II типа, отражает его оценку относительной валидности обоих типов обоснованности.
На пути к окончательным выводам остаются три трудные проблемы. Первая состоит в том, что только одного значимого различия недостаточно, если ожидается сильное влияние независимой переменной. Статистическая проверка наиболее пригодна в тех случаях, когда действие исследуемого фактора «зашумлено» другими случайными факторами. Вторая проблема заключается в том, что использование слишком большого числа испытуемых обнаруживает действие определенных дополнительных факторов. Третья проблема касается универсальности результатов. Можно ли отнести выводы ко всей соответствующей популяции, если они справедливы даже не для всех исследовавшихся испытуемых? Причем не только по причине случайных изменений. Наконец, было показано, что мы не можем принять экспериментальные выводы только на основе постоянных и достаточно сильных выявленных различий между условиями. Эксперименту будет недоставать внешней валидности, если он не будет удовлетворять хотя бы одному из целого ряда условий. Более того, он не будет обладать даже внутренней валидностью, если не организовать достаточный контроль за систематическим смешением.
ВОПРОСЫ
1. Почему Флинер и Кернс заключили, что старшие дети больше плачут при уходе матери, чем при уходе ассистентки, а у младших детей такого различия нет?
2. Что такое нуль-гипотеза?
3. Почему в эксперименте Флинера и Кернса возможно третье заключение, в то время как в эксперименте 259Иоки по предпочтению сорта томатного сока только два?
4. Что показывает диаграмма, иллюстрирующая: различие между средними для каждого условия, статистическое решение и заключение об экспериментальной гипотезе?
5. Как влияет уменьшение надежности на величину различия между средними, требуемую для отвержения нуль-гипотезы?
6. Как влияет альфа-уровень в правиле решения на величину различия между средними, требуемую для отвержения нуль-гипотезы?
7. Соотнесите альфа-уровень с риском ошибок I иII типов.
8. Когда особенно важно избегать ошибки I типа?
9. Опишите три фактора, влияющие на вероятность бета. Что это означает в отношении риска ошибки II типа?
10. При каких условиях экспериментатор может заключить, что независимая переменная не оказывает действия?
11. Почему говорят, что разумное использование правила статистического решения способствует внутренней валидности?
12. Может ли быть в эксперименте слишком много испытуемых?
13. Если в эксперименте получены надежные данные и высоко значимые различия между условиями, обеспечивает ли это полностью валидность вывода?
СТАТИСТИЧЕСКОЕ ПРИЛОЖЕНИЕ: t - КРИТЕРИЙ
В данном приложении будет описан метод нахождения величины различия между средними, необходимой для отвержения нуль-гипотезы. Фактически мы будем подробно объяснять диаграммы, представленные на рис. 6.1.
Выборочное распределение
Давайте еще раз предположим, что данные по времени реакции, представленные в предыдущих статистических приложениях, получены в межгрупповом эксперименте. Мы, таким образом, имеем среднее время реакции для каждого из 17 испытуемых, которым предъявлялось условие А (свет), и среднее время реакции для каждого из 17 испытуемых, которым предъявлялось условие Б (тон). Более того, известно общее среднее для испытуемых в условии А (185 мс) и общее среднее в условии Б (162 мс). Наконец, мы знаем разницу между этими двумя средними, МА—Мб, равную. +.23 мс.
Если бы исследовались две другие группы испытуемых, отобранные тем же способом, то, конечно, не следовало бы ожидать МА—Мб в точности равной 23 мс. Нельзя было бы ожидать точно такой же разницы + 23 мс и в третьем эксперименте. Напротив, мы предполагаем, что это значение МА—Мббудет несистематически варьировать от эксперимента к эксперименту.
Допустим, что путем повторения этого эксперимента был реализован бесконечный эксперимент, при котором каждое условие предъявлялось 17 испытуемым бесконечное число раз. Предположим далее, что нуль-гипотеза верна. Тогда различие между общими средними — которое есть параметр — должно равняться нулю. Другими словами, М̅А—М̅б=0. Однако величина статистики МА—Мбдолжна варьировать от эксперимента к эксперименту.
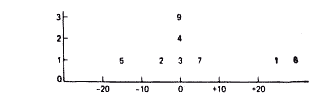
Распределение величин МА—Мбдля серии последовательных экспериментов может быть представлено так, как было описано ранее. Обозначим величину +23, которая была получена в реальном эксперименте, номером 1; предположим, что мы провели второй такой же эксперимент и получили величину — 4, обозначим ее номером 2; величину, полученную в третьем эксперименте (допустим, 0), — номером 3 и т. д. Таким образом, результаты девяти экспериментов, в случае МА—Мб = 0, могли бы выглядеть следующим образом.
|
|
| Рис , 6.2. Ось абсцисс —МА—Мб. Ось ординат — частота |
К счастью, можно вывести, как это распределение выглядело бы для бесконечного числа экспериментов. Мы можем реально изобразить ожидаемое распределение величин МА—Мб. Более того, мы можем оценить стандартное отклонение, которое имело бы это распределение. Такой тип теоретически выведенного распределения называют выборочным распределением. Описываемое здесь распределение является выборочным распределением разностей между средними (имеются также выборочные распределения для средних, для стандартных отклонений и т. д.).
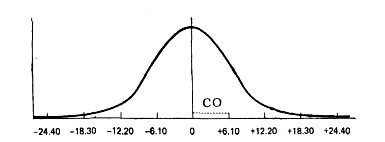
Приводим выборочное распределение для нашего эксперимента по времени реакции с предположением, что нуль-гипотеза М̅А—М̅б=0верна.
Заметьте, что стандартное отклонение (СО) равно 6,1.
|
|
| Рис . 6.3. Ось абсцисс —МА—Мб. Ось ординат — относительная частота |
Поэтому разность МА—Мб= +12,20, полученная в каком-то эксперименте, находится на расстоянии двух стандартных отклонений выше предполагаемой величины М̅А—М̅б = 0, а разность МА—Мб, равная —18,30, -- на три стандартных отклонения ниже предполагаемого нуля и т. д.
Стандартная ошибка
До сих пор не объяснялось, как было вычислено стандартное отклонение этого гипотетического выборочного распределения. Вот эта формула:
![]()
SmА-mБназывается стандартной ошибкой разности между средними. Использование термина стандартная ошибка вместо стандартного отклонения показывает, что мы вывели стандартное отклонение, а не пришли к нему через (невозможные) бесконечные вычисления. Заметьте, что здесь используется S, а не σ̅. Это потому, что популяционный параметр σ̅МА—МБоценивается на основе выборочных статистик.
Для вычисления в формулу просто подставляют величины S2A и S2Б, полученные нами в предыдущих статистических приложениях. Так,
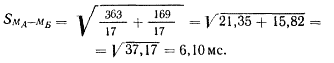
Вы можете видеть, что формула применима также и в том случае, когда NA и NБразличны, т. е. когда число испытуемых (или проб в интраиндивидуальном эксперименте) различно для двух условий.
Определение величины t
Следующий шаг состоит в том, чтобы найти, на сколько единиц стандартной ошибки отстоит полученная нами разность МА—Мбот нуля, представляющего среднюю нуль-гипотезы. Поскольку полученная нами разность равнялась +23, а стандартная ошибка МА—Мб=6,10, то очевидно, что наша разность находится на расстоянии 3,77 единицы стандартной ошибки выше нуля. Единицы стандартной ошибки называют t-едини-цами. Выражение полученной разности в единицах стандартной ошибки называют нахождением величины tдля данной разности. Это может быть выражено следующей формулой:
![]()
Подставляя значения из нашего эксперимента по измерению времени реакции, мы имеем
![]()
Заметьте, что нуль в числителе при числовых операциях можно опустить. Он служит для того, чтобы напомнить нам, что мы проверяем нуль-гипотезу:
М̅А—М̅б = 0.
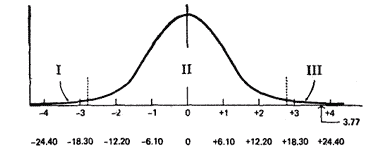
Отвержение или неотвержение нуль-гипотезы
Теперь мы готовы (наконец!) описать, как были получены диаграммы на рис. 6.1, показывающие величину
|
|
| Рис. 6.4. Ось абсцисс: первая—значения ί-критерия; вторая МА -ΜБ. Ось ординат — относительная частота. 1, III—р = 0,005, нуль-гипотеза отвергается; II—р=0,99, нуль-гипотеза не отвергается |
разности между средними, необходимую для отвержения нуль-гипотезы. Давайте перерисуем выборочное распределение разностей.
Вы найдете в Статистической таблице 2 вконце данного приложения величину t, достаточную для отвержения нуль-гипотезы. Она дана и для альфа-уровня 0,05, и для альфа-уровня 0,01. Эти критические величины зависят от величины N для каждого условия, или, иначе, от числа степеней свободы, N—1, для каждого среднего. (Если вы имеете данное среднее, скажем, 179 мс для 17 испытуемых, эта величина могла бы быть получена путем свободного приписывания любых величин 16 испытуемым. Однако затем вам придется приписать семнадцатому испытуемому совершенно определенную величину, чтобы получить заданное среднее.) Таким образом, поскольку было 17 испытуемых для каждого условия, имели место 16+16 = 32 степени свободы (или df).
В таблице нет значений именно для 32df(но величина для 30dfвполне годится, так как разница между величинами tдля 30 и 35dfочень мала. Чтобы отвергнуть нуль-гипотезу для 0,05 альфа-уровня, требуется t, равное 2,04, для альфа-уровня 0,01—t, равное 2,75. Величина t, равная в нашем эксперименте 3,77, показывает, что полученная разность +23 попадает в область отвержения, даже если использовать альфа-уровень 0,01.
Вероятности показаны так же, как на рис. 6.1 (в). Исходя из этого, наше статистическое решение будет заключаться в отвержении нуль-гипотезы.
Распределение, представленное в величинах t, является выборочным распределением t. Точная форма t-распределения будет разной в зависимости от числа степеней свободы в эксперименте. Вот почему вы должны находить критические величины, чтобы определить, является ли полученное вами различие значимым.
Нуль-гипотеза и ω2
Из данного статистического приложения видно, что в эксперименте по измерению времени реакций независимая переменная оказывала сильное влияние: estω2= = 0,28. Ясно, что получить такую разность между условиями в высшей степени невероятно, если верна нуль-гипотеза. Но не смешивайте эти два понятия — силу действия и статистическую значимость. При очень надежных данных даже небольшая разность между средними позволит отвергнуть нуль-гипотезу. В то же время разность может оказаться статистически значимой даже при слабом действии независимой переменной.
Задача: Вычислите tи проверьте нуль-гипотезу при альфа-уровне 0,01 для эксперимента по измерению времени реакции выбора между двумя вспышками света (условие В) и выбора между двумя тонами (условие Г).
| Условие | В (вспышки) | Условие | Г (тоны) | ||||
| Испыт. | ВР | Испыт. | ВР | Испыт. | ВР | Испыт. | ВР |
| 1 | 304 | 10 | 275 | 1 | 272 | 10 | 261 |
| 2 | 268 | 11 | 268 | 2 | 264 | 11 | 250 |
| 3 | 272 | 12 | 254 | 3 | 256 | 12 | 228 |
| 4 | 262 | 13 | 245 | 4 | 269 | 13 | 257 |
| 5 | 283 | 14 | 253 | 5 | 285 | 14 | 214 |
| 6 | 265 | 15 | 235 | 6 | 247 | 15 | 242 |
| 7 | 286 | 16 | 260 | 7 | 250 | 16 | 222 |
| 8 | 257 | 17 | 246 | 8 | 245 | 17 | 234 |
| 9 | 279 | 9 | 251 |
Ответ: Мв=265; Мг=250; S2B=292; 52Г=337; t=2,47.
Нуль-гипотеза может быть отвергнута при альфа-уровне 0,05, но не при альфа-уровне 0,01.
Статистическая таблица 2.
Величина t-критерия, отвергающая нуль-гипотезу
| Степень свободы df | 0,05 | 0,01 | Степень свободы df | 0,05 | 0,01 |
| 1 | 12,71 | 63,66 | 24 | 2,06 | 2,80 |
| 2 | 4,30 | 9,92 | 2Б | 2,06 | . 2,79 |
| 3 | 3,18 | 5,84 | 26 | 2,06 | 2,78 |
| 4 | 2,78 | 4,60 | 27 | 2,05 | 2,77 |
| 5 | 2,57 | 4,03 | 28 | 2,05 | 2,76 |
| 6 | 2,45 | 3,71 | 29 | 2,04 | 2,76 |
| 7 | 2,36 | 3,50 | 30 | 2,04 | 2,75 |
| 8 | 2,31 | 3,36 | 35 | 2,03 | 2,72 |
| 9 | 2,26 | 3,25 | 40 | 2,02 | 2,71 |
| 10 | 2,23 | 3,17 | 45 | 2,02 | 2,69 |
| 11 | 2,20 | 3,11 | 50 | 2,01 | 2,68 |
| 12 | 2,18 | 3,06 | 60 | 2,00 | 2,66 |
| 13 | 2,16 | 3,01 | 70 | 2,00 | 2,65 |
| 14 | 2,14 | 2,98 | 80 | 1,99 | 2,64 |
| 15 | 2,13 | 2,95 | 90 | 1,99 | 2,63 |
| 16 | 2,12 | 2,92 | 100 | 1,98 | 2,63 |
| 17 | 2,11 | 2,90 | 120 | 1,98 | 2,62 |
| 18 | 2,10 | 2,88 | 150 | 1,98 | 2,61 |
| 19 | 2,09 | 2,86 | 200 | 1,97 | 2,60 |
| 20 | 2,09 | 2,84 | 300 | 1,97 | 2,59 |
| 21 | 2,08 | 2,83 | 400 | 1,97 | 2,59 |
| 22 | 2,07 | 2,82 | 500 | 1,96 | 2,59 |
| 23 | 2,07 | 2,81 | 1000 | 1,96 | 2,58 |
| оо | 1,96 | 2,58 |
Статистическая таблица 2 взята из таблицы IV в работе Фишера и Ятса «Статистические таблицы для биологических, сельскохозяйственных и медицинских исследований».
Количество статей: 1
Статьи
Информация об авторе: Роберт Готтсданкер
Опубликовано: January 4, 2005, 12:35 am